【三平方の定理】 立方体で最短距離を求める問題の解き方
立方体や直方体に糸をかける問題で,その最短距離を求める問題の解き方がわかりません。
進研ゼミからの回答
最短距離は展開図を使って考えましょう。
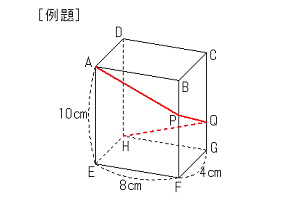
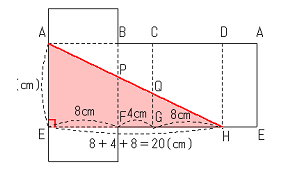
頂点Aから頂点Hまで上の図のように糸を巻きつけ、辺BFとの交点をP、辺CGとの交点をQとする。
AP + PQ + QHがもっとも短くなるときの糸の長さを求めなさい。
■展開図をかく
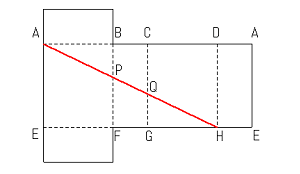
[図1] のように、
点Aから点Hまでが辺BF、辺CGを通って直線でつながる展開図をかきましょう。
※[図2] のように、点Aから点Hまで進むと途中で切れてしまう展開図ではダメです。

■直線で結ぶ
最短距離になるのは、
点A、P、Q、H、が一直線上であるときです。
よって、点Aから点Hまでを直線で結んだ線分AHの長さが、AP + PQ + QHの最短距離となります。
■AHの長さを求める
線分AHの長さは三平方の定理を使って求めます。
三平方の定理より、AH2 = AE2 + EH2
AH2 = 102 + 202
= 100 + 400
= 500
AH = ±
= ±10
AH > 0 より、
AH = 10(cm)